Prior to the ATC training, recently held in Fort Collins, there were a number of home work problems assigned. Tim Whitehouse, Journeyworker and owner of Arris Timberworks, has spent some time with the Compagnon du Devoir in France, working specifically on developed drawing. He offered the following solution and lesson related to the homework problem of inscribing an octagon on a circle.
Before beginning this exercise, a couple of simple, but important geometric constructions need be explained.
Bisecting a line Fig.1
Take any line AB. Set your compass to more than 1/2 the length Line AB. With the point of the compass on A, swing an arc above and below the Line AB. From point B do the same. Draw a line from the intersections of these arcs. This line is the perpendicular bisector of line AB
-
- Figure 1
-
- Figure 2
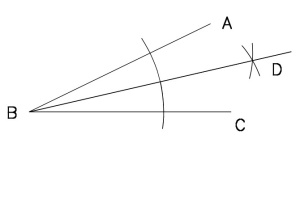
Bisecting an angle Fig. 2
Take any angle ABC. Swing an arc from point B(the Vertex) and intersect Line BA and Line BC. From the arc intersection on each line, swing another set of arcs. Draw a line from the Vertex B to point D. This line bisects the angle ABC
The first homework problem was to inscribe an octagon in a circle using pencil, straight edge and a compass.
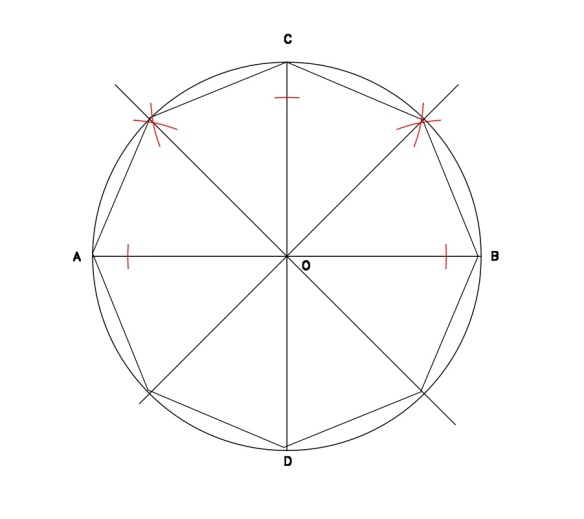
Inscribing an octagon in a circle Fig. 3
Draw a circle with the Center O. Draw the diameter, Line AB. Bisect Line AB, giving you Line CD. Bisect Angles AOC and BOC (red construction lines in Fig 3). Connect the intersections of these radii and the circle to complete the construction.
Figure 3
What is the practical value of this? Understanding simple geometric principles can allow one to solve complex problems with very low tech tools. In regards to carpentry, the octagon is seen in posts and is probably the most common form of polygonal plan after the rectangle.
Other ways to create octagons:
The octagon scale, available on some framing squares, allows a quick layout for an octagonal post from a square timber.
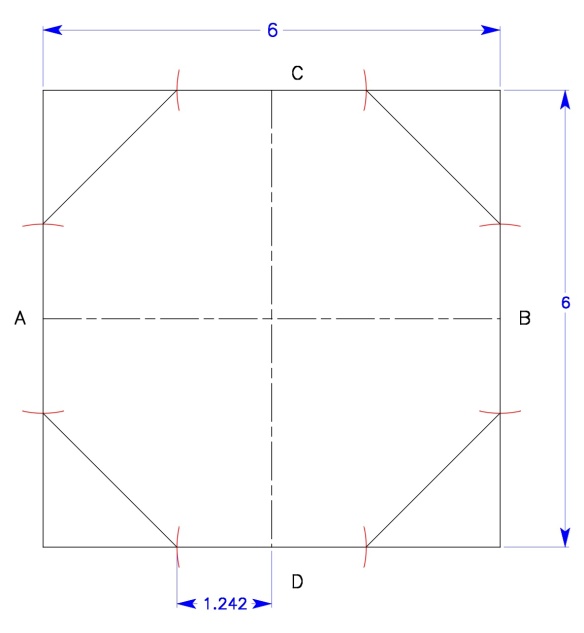
For example, if you wished to make an octagonal post from a 6 x 6 timber. Set your compass to 6 on the octagon scale. (Fig. 4)
Figure 4
Swing this arc (red construction lines) from the midpoints (labeled A,B,C, D) of the sides your timber,. (Fig. 5.)
Figure 5
The math solution for the length of the arc for the above.
Arc length = width of timber * .207
6 * .207= 1.242”
TFG Apprenticeship 